Conway's Game Of Life is a cellular atomaton that was devised by British Mathematician John Horton Conway. The "game" is played by having a user interact with the "board" to create an initial configuration, and then observe how it evolves. The game evolves by following 3 basic rules:
- Alive cells with less than 2 Neighbors die
- Alive cells with more than 3 Neighbors die
- Dead cells with 3 neighbors become alive
Some woud include a 4th rule stating that "Any live cell with two or three live neighbours lives on to the next generation." I have a hard time listing it as a specific rule, as the case is already handled with the existence of the other 3 rules. It seems redundant and unnecessary to explicitely list, since one doesn't have to specifically implement that rule to get the desired behavior.
This implementation was created utilizing JavaScript and the HTML5 canvas. A basic grid is created with basic mouse event handlers. Each frame the program will traverse the grid and determine the state of each cell by checking the state of all eight neighbors. Then I determine if the cell is in a state of change (from dead to alive, and vice versa). If the state is changing, then I add the cell location to an array of cells to be given life or given death. Once the entire grid has been checked we can advance the generation by traversing both arrays and toggle the cells setting to alive/dead. This then completes the iteration of the frame, and we are ready to move onto the next frame and restart the process.
In the case of a "Closed World" setting the edge cells treat all non-existent neighbors as being dead. This results in artifacts when cells become active around the boarder, such as the gliders turning into the Block Pattern. In the case of a "Wrapped World" setting, the edge cells "wrap" around and check the cells on the other end of the grid. This also creates artifacts and undesired behavior when gliders and other Spaceships approach the corners of the grid.
There are many types of patters that have been discovered in Conway's Game Of Life. Three types of patters are Still Lifes, Oscillators, and Spaceships. The patterns I utliize in my default state are Gosper's Glider Gun, Toad, and a single Glider.
A still life is a pattern that has found balance and remains in a constant state during each itteration. Popular Still Life examples are the Block, Beehive, and Loaf.

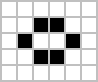
Oscillators repeat the same pattern over generations. Some, such as the Blinker and Toad, repeat themselves over 2 generations. Others, such as the Pulsar and (to a point) Gosper's Glider Gun, repeat after multiple generations have passed.


Spaceships are patterns that can move along the grid and travel from their point of origin. The Glider is a perfet example of this pattern. While Gosper's Glider Gun is essentially an oscillator, it's "function" is to produce Gliders that are "shot" out into the environment and will move in a straight line until encountering other patterns. These patterns will move themselves as the generations itterate.
